

Given any point on an extended body, if there is a force acting on the body that does not travel through that point, then that force will cause a moment about that point. As discussed on the moments page, a moment is a force's tendency to cause rotation.
An alternative to calculating the moment via scalar quantities is to use the vector method or cross product method. For simple two-dimensional problems, using scalar quantities is usually sufficient, but for more complex problems the cross product method tends to be easier. The cross product method for calculating moments says that the moment vector of a force about a point will be equal to the cross product of a position vector \(\vec\), from the point to anywhere on the line of action of the force, and the force vector itself. \[ \vec \, = \, \vec \times \vec \] A big advantage of this method is that \(\vec\) does not have to be the shortest distance between the point and the line of action; it goes from the point to any part of the line of action. For any problem, there are many possible \(\vec\) vectors, but because of the way the cross product works, they should all result in the same moment vector in the end.  It is important to note here that all quantities involved are vectors: \(\vec, \, \vec\), and \(\vec\). Before you can solve for the cross product, you will need to write out \(\vec\) and \(\vec\) in vector component form. You will need to write out all three components of these vectors: for two-dimensional problems their \(z\) components will simply be zero, but those values are necessary for the calculations. The moment vector you get will line up with the axis of rotation for the moment, where you can use the right-hand rule to determine if the moment is going clockwise or counterclockwise about that axis.
It is important to note here that all quantities involved are vectors: \(\vec, \, \vec\), and \(\vec\). Before you can solve for the cross product, you will need to write out \(\vec\) and \(\vec\) in vector component form. You will need to write out all three components of these vectors: for two-dimensional problems their \(z\) components will simply be zero, but those values are necessary for the calculations. The moment vector you get will line up with the axis of rotation for the moment, where you can use the right-hand rule to determine if the moment is going clockwise or counterclockwise about that axis. 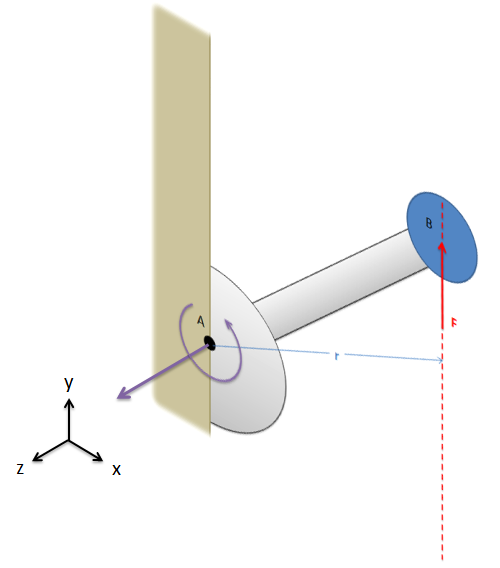 Finally, it is also important to note that taking the cross product, unlike multiplication, is not communicative. This means that the order of the vectors matters, and \(\vec \times \vec\) will not be the same as \(\vec \times \vec\). It is important to always use \(\vec \times \vec\) when calculating moments.
Finally, it is also important to note that taking the cross product, unlike multiplication, is not communicative. This means that the order of the vectors matters, and \(\vec \times \vec\) will not be the same as \(\vec \times \vec\). It is important to always use \(\vec \times \vec\) when calculating moments. .png?revision=1) Solution
Solution .png?revision=1) connects the top of an upright 15-foot-high pole to the ground. The location where the end of the cable touches the ground is 15 feet behind the spot that is 3 feet to the right of the base of the pole." />Solution
connects the top of an upright 15-foot-high pole to the ground. The location where the end of the cable touches the ground is 15 feet behind the spot that is 3 feet to the right of the base of the pole." />Solution
Video \(\PageIndex<3>\): Worked solution to example problem \(\PageIndex\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/ioqy98jZ0Vg.
This page titled 3.4: Moment about a Point (Vector) is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Jacob Moore & Contributors (Mechanics Map) via source content that was edited to the style and standards of the LibreTexts platform.